Logic circuits and software

Logic circuits and software	Toshiyuki Masui
	2018/7/11
	http://Scrapbox.io/masui

Reasons why we should study logic circuits
	Simply interesting
	Understanding boolean logic (switching algebra)
	Making Ubicomp hardware
	Understanding state transition machines

Steve Wozniak
	
	Apple cofounder
	Logic circuit wizard
	Designed sophisticated systems with elegant design

AppleII Schematic
	

Masui's article (1978)
	

A computer is ...
	A very complex state transition machine
	State changes based on current state and external conditions
		clock signal (= time)
		interrupt signals
		sensor values
	Made up of digital logic circuits

State diagram of a toggle switch
	

State transition of puzzle pieces
	

Detecting C-style comments
	Recognize  /*  ....  */ 
	

Typical structure of a hardware state transition machine
	A memory device for holding current status
	Combinational circuits for calculating next state
	External input
	

Example: digital clock
	Input =  pulses from AC outlet
		50Hz pulse
	Changing the value every  second
	Users can set values

Turing Tumble
	

Digital circuits
	Combinations of on/off switches
	Can be constructed using relays and other hardware
	Combinational logic and Sequential logic

Combinational logic
	No memory
	Like a pure function
		AND, OR 
		Adder
		 

Example: AND function
and.cCopied!
function and(x,y){
  if(x == 1 && y == 1) return 1;
  else return 0;
}

MIL symbol of an AND gate
	

AND logic example
	Implementation with relays (electromagnet + switch)
	

MIL symbol of an OR gate
	

OR logic example
	

MIL symbol of a NOT gate
	

MIL symbol of an AND gate
	NAND = AND + NOT
	

A TTL NAND gate
	

SN7400N
	TTL from Texas Instruments
	

SN7400N
	


CMOS NAND gate
	

Exclusive OR
	

EOR gate from NAND gates
	

Truth table of an NAND gate
	

Karnaugh map
	

Karnaugh map of an OR gate
	

Adder
	

Half adder
	


Full adder
	 

Full adder
	


Comparator
	

Karnaugh map of a compare function
	AB > CD ?
	

Optimizing the circuit using a Karnaugh map
	Find large rectangles which fits the pattern
	

Corresponding if-statement
	Listing all the conditions
	 if(A == 1 && C == 0 || 
		 C == 0 && D == 0 && B == 1 || 
		 A == 1 && B == 1 && C == 1 && D == 0) 
	Difficult without a Karnaugh map

Disjunctive normal form (DNF)
	

PLA-based DNF Implementation
	

Sequential Logic

How can we hold current state?
	Use Flip-Flops
	Can have stable values
	Combinational logic with feedback wiring

RS Flip-Flop
	

D Latch
	

D Flip-Flop
	Can be used as a memory device
	

CMOS Switch
	

D Flip-Flop on CMOS
	

State transition machine
	

Counter
	

Shift register
	

Fluctuation LED
	
	Using a shift register
	Generate pseudo-random values using M-series
	

Simulation of M-series
	Use P5.js
	Run
m.jsCopied!
function setup(){
  data = []
  createCanvas(640,20)
  for(i=0;i<32;i++) data[i] = 0
  frameRate(20)
}
function draw(){
  strokeWeight(0)
  for(i=0;i<1;i++){
    data.push((data[3] + data[10] + data[29] + 1) % 2) //
    data.shift()
  }
  for(i=0;i<32;i++){
    fill(data[i] == 0 ? 'black' : 'white')
    rect(i*20,0,20,20)
  }
}

State transition programming
	Using the current execution point
		Using the program counter as the state variable
	Using state variables
	Using a state transition table

Flowchart
	

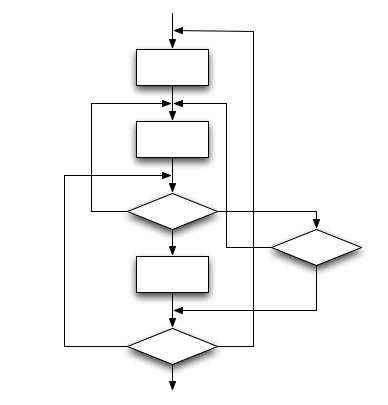
Recognizing C comments
	 /*  ...  */ 
	

Using the execution point as the state variable
comment1.cCopied!
#include <stdio.h>
main()
{
  int c;
  while(1){
    c = get_c();
    while(c == '/'){
      c = get_c();
      if(c == '*'){
        printf("/*");
        int done = 0;
        while(! done){
          c = get_c();
          printf("%c",c);
          while(c == '*'){
            c = get_c();
            printf("%c",c);
            if(c == '/'){
              done = 1;
              c = get_c();
              break;
            }
          }
        }
      }
    }
  }
}

Characteristics of this approach
	Good for simple cases
	Not good for very complicatd state transition
		Difficult to understand in many cases

Using state variables
	Combination of values indicate the state of the program
	Using if's and switch's for state transition table
	Good for simple state transition
	Not ideal for really complicated state transition

comment2.c
comment2.cCopied!
typedef enum {
 S1, S2, C1, C2
} State;
State state = S1;
trans(int c)
{
  switch(state){
  case S1:
    if(c == '/') state = S2;
    break;
  case S2:
    if(c == '/') state = S2;
    else if(c == '*'){
      printf("/*");
      state = C1;
    }
    else state = S1;
    break;
  case C1:
    printf("%c",c);
    if(c == '*') state = C2;
    break;
  case C2:
    printf("%c",c);
    if(c == '*') state = C2;
    else if(c == '/') state = S1;
    else state = C1;
    break;
  }
}
main()
{
  char buf[1000];
  char *s;
  while(fgets(buf,1000,stdin)){
    for(s=buf;*s;s++){
      trans(*s);
    }
  }
}

Using a state transition table
	Assign a unique number to each state
	Create a state transitino table
		By hand
		By special tools

State transition table
	

comment3.c
comment3.cCopied!
enum {
  S1, S2, C1, C2
};

int trans[4][0x100];
int state = S1;

void init()
{
  int i;
  for(i=0;i<0x100;i++){
    trans[S1][i] = S1;
    trans[S2][i] = S1;
    trans[C1][i] = C1;
    trans[C2][i] = C1;
  }
  trans[S1]['/'] = S2;
  trans[S2]['/'] = S2;
  trans[S2]['*'] = C1;
  trans[C1]['*'] = C2;
  trans[C2]['*'] = C2;
  trans[C2]['/'] = S1;
  state = S1;
}

main()
{
  unsigned char buf[1000];
  unsigned char *s;
  init();
  while(fgets(buf,1000,stdin)){
    for(s=buf;*s;s++){
      int oldstate = state;
      state = trans[state][*s];
      if(oldstate == S2 && state == C1) printf("/*");
      if(oldstate == C1 || oldstate == C2) printf("%c",*s);
    }
  }
}


State transition programming ≈ state transition machine
	

State transition programming and Karnaugh map
	
	

Conclusions
	Logic circuits are not only important, but interesting
	Circuits and software for state transition are important
	Various techniques are common to hardware and software

AppleII Schematic
	


#講義資料
Logic circuits and software

関連ページ
